Memoire SAVARY LEMONT

Processus stochastique
Un processus stochastique est une famille de variables aléatoires, généralement indexée par $\mathbb R^+$ ou $\mathbb N$ .

Filtration
Une filtration est une suite croissante de tribus $(\mathcal{F}_n)_{n\ge 0}$ , c'est-à-dire $\mathcal{F}_n \subset \mathcal{F}_{n+1} \ \ \forall n \in \mathbb N$

Filtration naturelle
Soit $(X_n)_{n \ge 0}$ une suite de variables aléatoires. On dit que $(\mathcal{F}_n)_{n\ge 0}$ définie par $\mathcal{F}_n = \sigma (X_1,\ldots ,X_n) \ \forall n \in \mathbb N$ est la filtration naturelle de la suite $(X_n)_{n \ge 0}$ .

Processus adapté
On dit que le processus $(X_n)_{n \ge 0}$ est adapté à la filtration $(\mathcal{F}_n)_{n\ge 0}$ si Xn est $\mathcal{F}_n -mesurable$ pour tout entier n.

Martingale dans $\mathbb{N}$
Soit $(\mathcal{F}_n)_{n\ge 0}$ une filtration.
Soit $(M_n)_{n \ge 0}$ une suite de variables aléatoires.
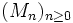On dit que $(M_n)_{n \ge 0}$ est une martingale par rapport à $(\mathcal{F}_n)_{n\ge 0}$ si:

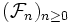$(M_n)_{n \ge 0}$ est adaptée à la filtration $(\mathcal{F}_n)_{n\ge 0}$ .

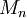$M_n \,$ est intégrable pour tout entier n.

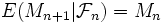$E(M_{n+1} | \mathcal{F}_n ) = M_n$ .

Si $(M_n)_{n \ge 0}$ respecte les deux premières conditions, et $E(M_{n+1} | \mathcal{F}_n ) \ge M_n \ \forall n$ alors on l'appelle sous-martingale, et si $E(M_{n+1} | \mathcal{F}_n ) \le M_n \ \forall n$ , alors on l'appelle sur-martingale.
On dit que $(M_n)_{n \ge 0}$ est une $\mathcal{F}_n$ -martingale.

Processus prévisible
Soit $(\mathcal{F}_n)_{n\ge 0}$ une filtration.
Soit $(Y_n)_{n \ge 0}$ une suite de variables aléatoires.
On dit que $(Y_n)_{n \ge 0}$ est processus prévisible si $Y_0 \,$ est $\mathcal{F}_0$ -mesurable et $Y_{n+1} \,$ est $\mathcal{F}_n$ -mesurable pour tout entier n.

Définition du mouvement brownien
Le mouvement brownien est un processus Gaussien, à accroissements indépendants et stationnaires: son accroissement Wt − Ws (0 _ s < t) suit une loi gaussienne centrée, de variance (t − s).
Bref historique. C’est en 1827 que le mouvement brownien est associé aux trajectoires tr`es irrégulières (en fait non dérivables comme fonctions du temps) de fines particules dans un fluide par le botaniste Robert Brown ; en 1900, Louis Bachelier l’utilise pour modéliser la dynamique des cours boursiers, puis Einstein en 1905, pour d´écrire une particule qui diffuse. Ce n’est qu’en 1923 que Wiener formalise sa construction. C’est le début de recherches mathématiques intensives qui se poursuivent toujours aujourd’hui et irriguent
une large part des probabilités modernes.