Principe et hypothèses du modèle de Black Scholes
C'est le modèle le plus répendu dans les milieux bancaires et financiers. Il sert au pricing d'option à temps continu, il est basé sous les hypothèses suivante:
-Taux d’intérêt sans risque fixe quelle que soit l’échéance
-Absence d’opportunité d’arbitrage
-Titre parfaitement divisible
-Transaction continues sans cout
-Cours du sous jacent qui suit un mouvement brownien
-Option Européennes
-Rendement normal
-Volatilité implicite
Equation différentielle de Black Scholes
EDP de Black Sholes : ![]()
Avec la condition au bord : f(T,s) = fT(s)
Formule de Feynman-Kac et évaluation à risque neutre
Dans un contexte de pricing d’option européen basé sur S sous l’hypothèse risque neutre la formule de Feynman Kac nous donne la relation suivante:
F(s,t) =exp(-r(T-t)) Eq(f(T,ST)|St=s)
où Eq représente l'espérance calculée dans le monde risque-neutre.
Formule de Black Sholes
La formule théorique du prix du call donnée par black Scholes avec un Payoff (St-K)+ est à l’instant t:
C(S,K,r,t,σ)= S. N(d1)- Kexp(-r(T-t)) N(d2)
De même, le prix théorique d'une option de vente, de pay off (K-St)+ est donné par :
P(S,K,r,t,σ)= - S. N(-d1)+ Kexp(-r(T-t)) N(-d2)
avec
- la fonction de répartition de la loi normale centrée réduite N(0,1), c'est-à-dire
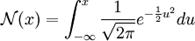
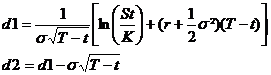
Les différents indicateurs
1- Le Delta
![]()
2- Le Omega
3- Le Gamma
![]() où
où ![]()
4- Le Thêta
![]()
5- Le Vega
![]()
6- Le Rhô
![]()
Simulation sous Excel et en VBA
Les fonctions Call_BS et Put_BS qui permette de calculer, le prix des option européennes Call et Put, les paramètres à rentrer par le modèle sont : So, la volatilité, le taux sans risque, strike, échéance et t l’instant voulu (pour le prix de l’option t=0)
Function Call_BS(s As Double, v As Double, r As Double, k As Double, tn As Double, t As Double) As Double
Dim cs As Double
Dim dx1 As Double
Dim dx2 As Double
Dim nd1 As Double
Dim nd2 As Double
dx1 = 1 / (v * Sqr(tn - t)) * (Log(s / k) + (r + 0.5 * v * v) * (tn - t))
dx2 = dx1 - v * Sqr(tn - t)
nd1 = WorksheetFunction.NormSDist(dx1)
nd2 = WorksheetFunction.NormSDist(dx2)
cs = s * nd1 - Exp(-r * (tn - t)) * nd2 * k
Call_BS = cs
End Function
Function Put_BS(s As Double, v As Double, r As Double, k As Double, tn As Double, t As Double) As Double
Dim ps As Double
Dim dx1 As Double
Dim dx2 As Double
Dim nd1 As Double
Dim nd2 As Double
dx1 = 1 / (v * Sqr(tn - t)) * (Log(s / k) + (r + 0.5 * v * v) * (tn - t))
dx2 = dx1 - v * Sqr(tn - t)
nd1 = WorksheetFunction.NormSDist(-dx1)
nd2 = WorksheetFunction.NormSDist(-dx2)
ps = -s * nd1 + Exp(-r * (tn - t)) * nd2 * k
Put_BS = ps
End Function